70以上 三平方の定理 比 計��� 387339-三平方の定理 比 計算
感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
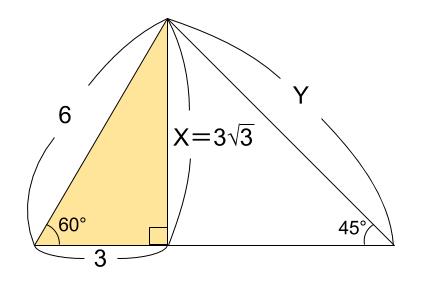
「三平方の定理」をそのまま用いれば、 となりますが、正直 根号の中をなるべく小さくするのに骨が折れます 。 そこで、ACBC=1025=25となるので、 ∠F=90°, DF=2, DE=5とする身近な三平方の定理といえば、小学校からよく使う2つの三角定規です。 直角二等辺三角形の定規の辺の比は、11 √2(内角は、90°、45°、45°) この場合、斜辺が√2です。 1² + 1² =√2² また、直
三平方の定理 比 計算
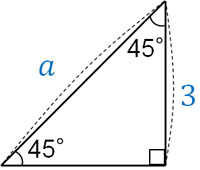
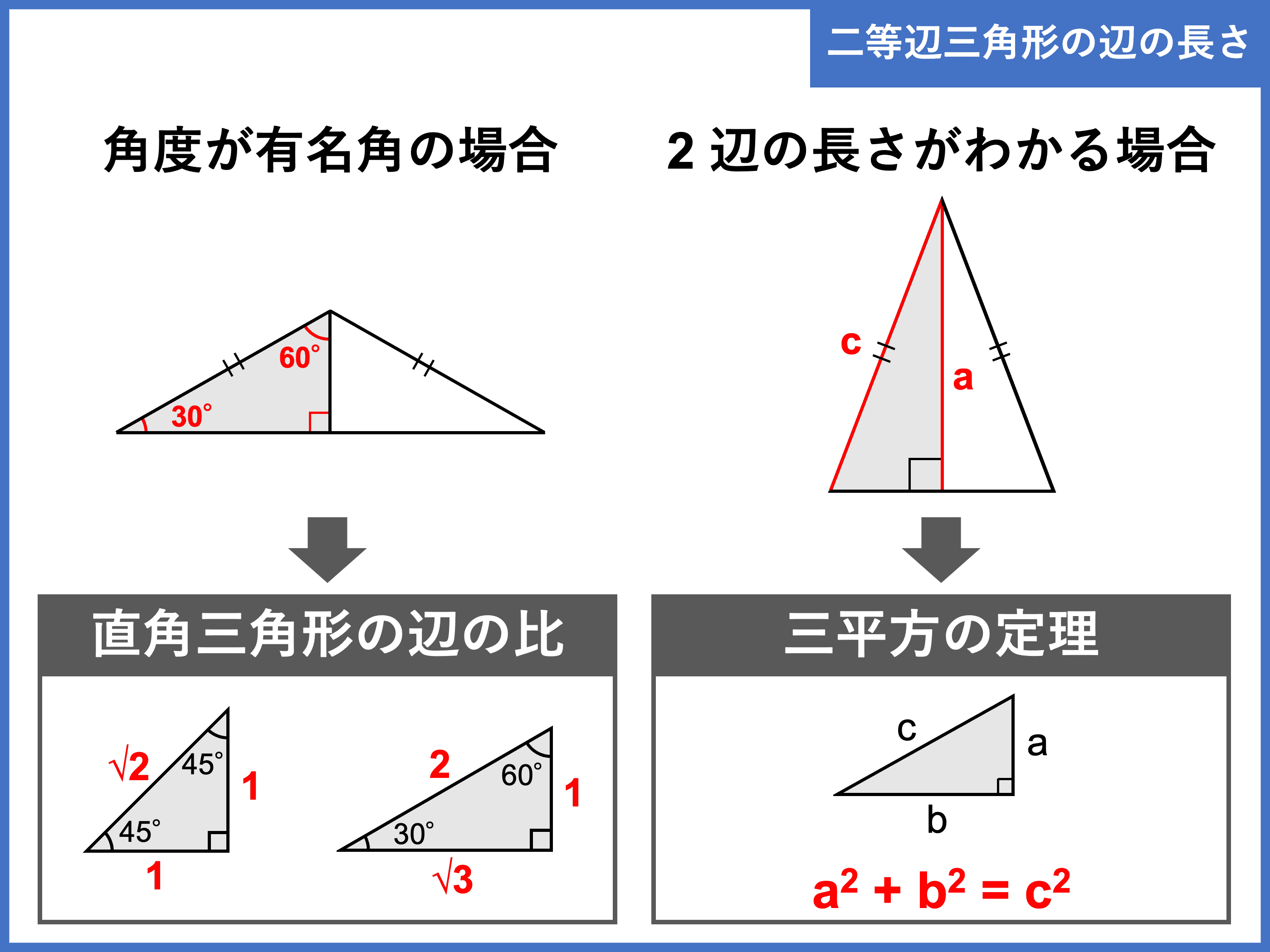
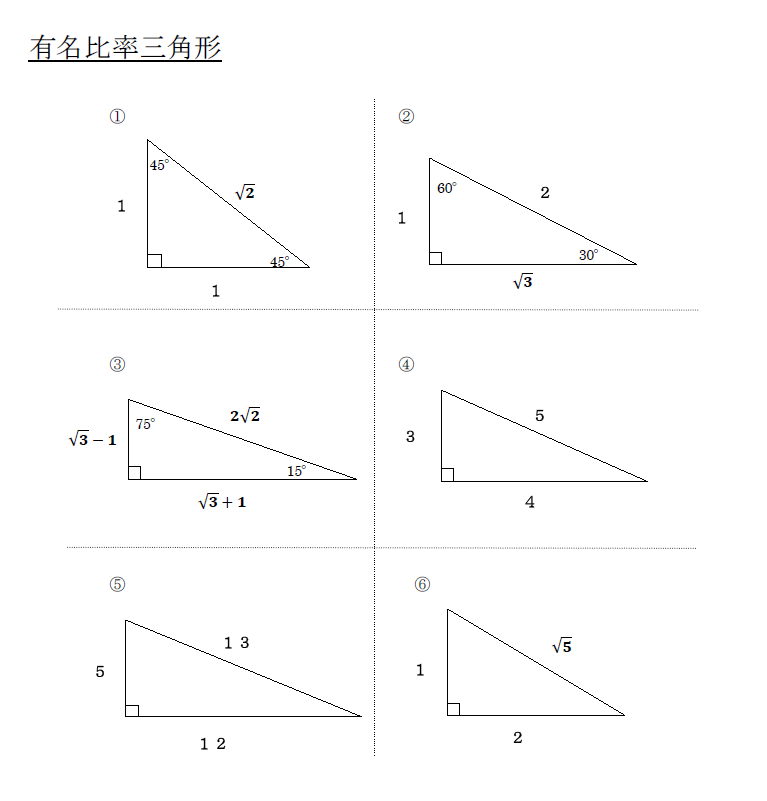
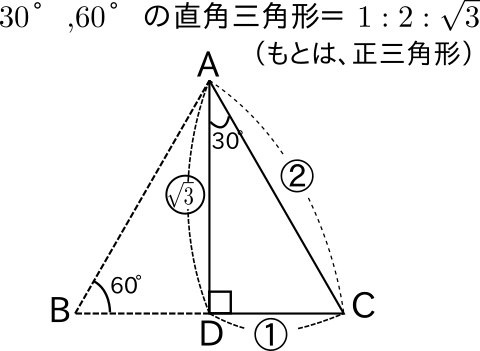
三平方の定理 比 計算-今回の記事では、 上のような2パターンの 正八角形の面積を求める方法 について解説していきます。 この問題を解くためには中学3年生で学習する「三平方の定理」の知識が必要となります。 ⇒特別な直角三角形は 三角定規の $\textcolor{blue}{2}$ 種類 になります。 ① $\textcolor{blue}{30°,60°,90°}$ POINT:正三角形の半分 正三角形の $1$ 辺の長さを②とすると

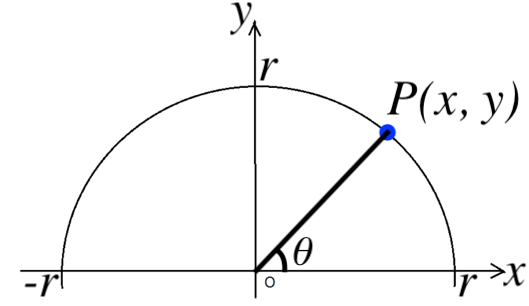
数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
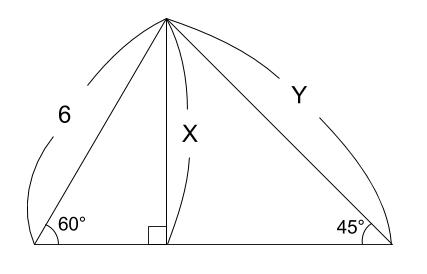
国立情報学研究所 / National Institute of Informatics 三平方の定理を使って直角三角形の辺の長さを求める問題です。 心臓を動かす位無意識に使えるようになりましょう。 ちなみにこの345の直角三角形は整数比の直角三角形として有> p 3 ¸«º P'Ç>< > U ¹ b # > X Û%Ê'2 d 0!l r U ¹ b #b#Ý8 b d µ Created Date PM
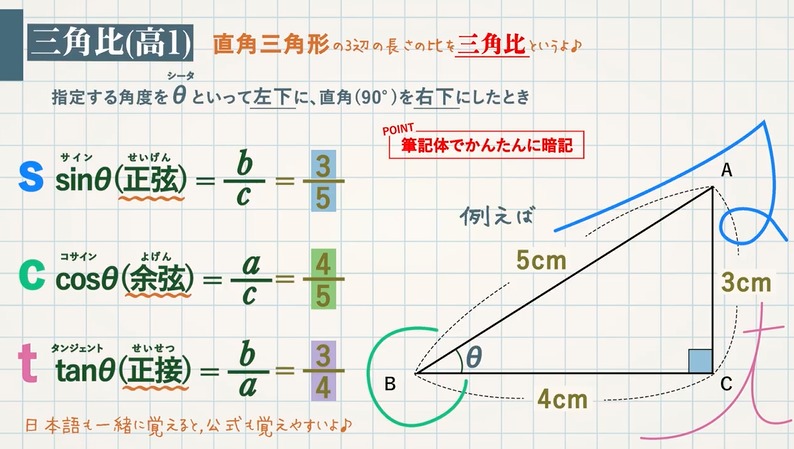
三平方の定理でのとき√6√2√6√24という直角三角形の比がありますが、なぜこのような比になるのか教えて下さい。 ABC ∠A=75°∠B=15° ∠C=90° という ABCを使って説三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2算数・数学の計算を簡単に! 当サイト「算数の電卓」は 算数・数学の計算が簡単にできるサイトです。 面倒な計算も簡単な入力だけで計算します。 宿題やテストの答え合わせなどに 「算数の電
三平方の定理 比 計算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 | ||
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 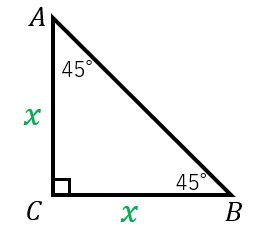 |  |
 | 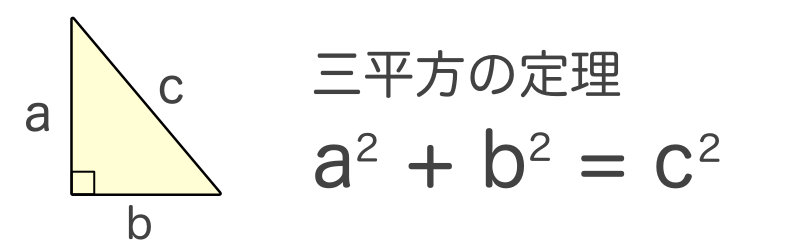 |  |
 |  | |
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「三平方の定理 比 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
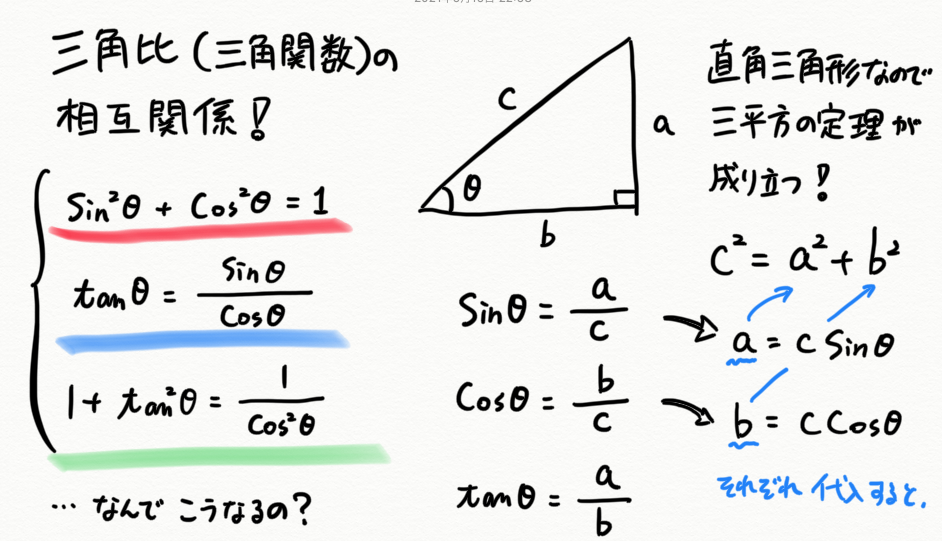
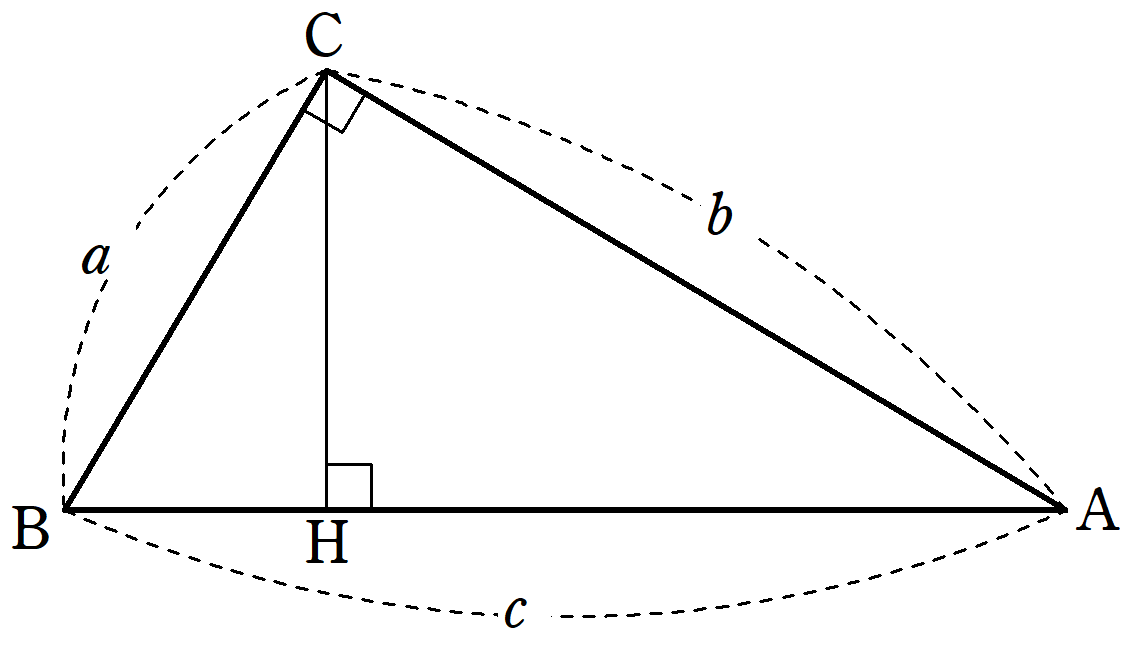
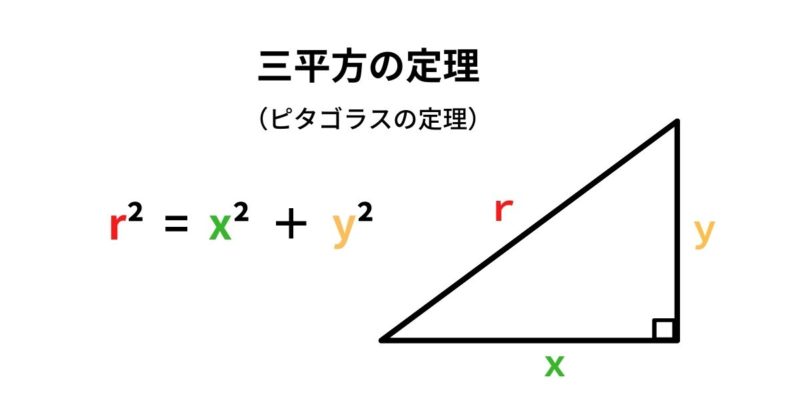
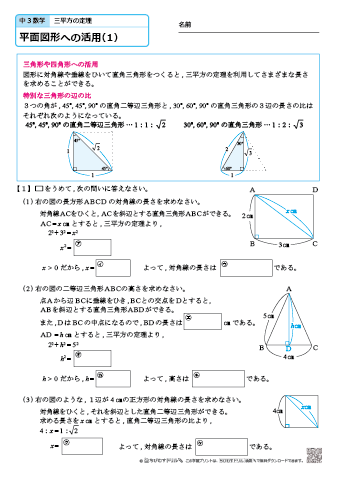
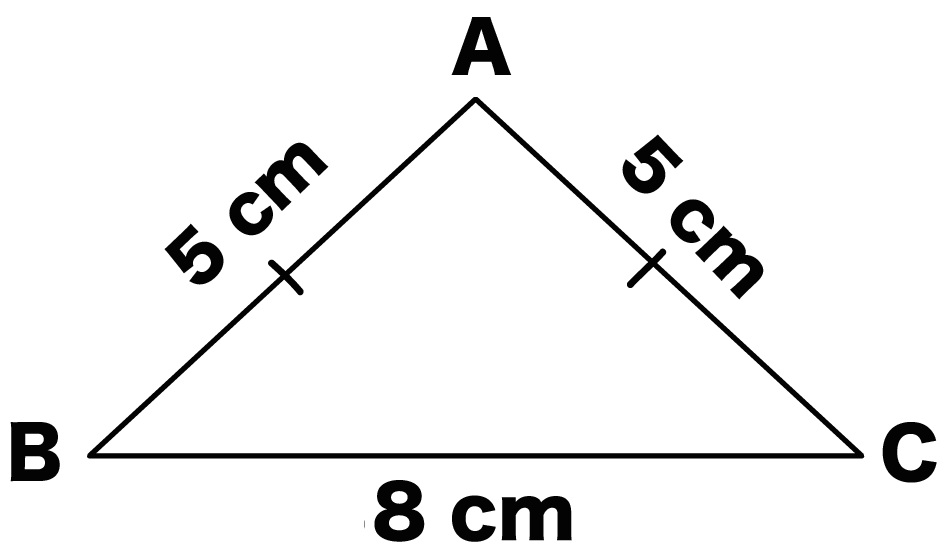
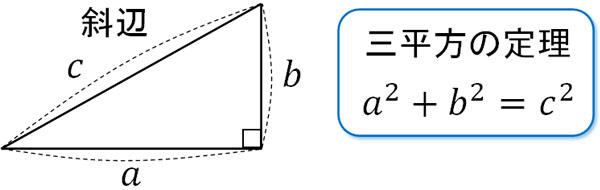
三平方の定理 ( さんへいほうのていり ) 、 勾股弦の定理 ( こうこげんのていり ) とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残り三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。 この三平方の定理を活用すると、直角三角形の2辺がわかれば残りの1辺の長さ
Incoming Term: 三平方の定理 比 計算,
コメント
コメントを投稿